[자료구조]Tree
트리는 노드로 이루어진 재귀적 자료 구조이다
이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조이다
트리는 하나의 루트 노드를 갖는다.
노드(node)들과 노드들을 연결하는 간선(edge)들로 구성되어 있다
노드가 n개인 트리는 항상 n-1개의 간선(edge)을 가진다
트리에는 사이클(cycle)이 존재할 수 없다.
노드들은 특정 순서로 나열될 수도 있고 그럴 수 없을 수도 있다.
각 노드는 부모 노드로의 연결이 있을 수도 있고 없을 수도 있다.
각 노드는 어떤 자료형으로도 표현 가능하다.

| Node | LinkedList와 비슷하게 tree에도 node가 존재한다. 각 node는 데이터를 포함하고 있다 |  |
| Parent(부모) Child(자식) |
부모노드는 다수의 자식 노드를 가지고 있을수 있다 하지만 자식 노드는 하나의 부모만 가진다 |  |
| 루트 노드(Root) | 트리에 가장 상단에 위치한 노트 이다 부모가 없고 트리는 하나의 루트 노드만을 가진다 |
 |
| 단말 노드(Leaf) | 자식이없는 노드입니다. 트리에 가장 끝부분에 위치한다 |  |
| 노드의 크기(Size) | 자신을 포함한 자식 노드의 수 | Size = 6 |
| 노드의 깊이(Depth) | 루트에서 특정노드 까지 도달하는데 거쳐야하는 간선의 수 |
B의 깊이 1 E의 깊이 2  |
| 노드의 레벨(Level) | 트리에 특정 깊이를 가진 노드의 집합 | A의 레벨 1 B와 C의 레벨 2 D E F 레벨 3  |
| 노드의 차수(Degree) | 각 노드가 가진 가지의 수 | B의 차수: 3 A의 차수 2  |
| 트리의 차수 | 트리의 최대 차수 | B가 가장 많은 가지수를 가지고있기 때문에 트리의 차수는 3  |
| 트리의 높이 | 루트 높이에서 가장 깊이있는 노드의 깊이 | 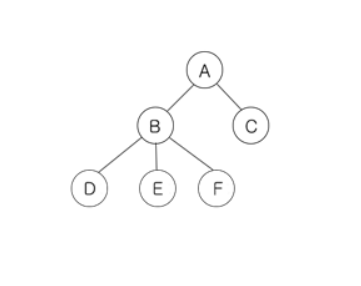 |
이진 트리(Binary tree)
자식 노드가 최대 두 개인 노드들로 구성된 트리
두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있다
이진 트리는 자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나뉜다
- 포화 이진 트리(full binary tree) : 각 레벨에 노드가 꽉 차 있는 이진 트리로, 각 노드에 레벨 단위로 왼쪽에서 오른쪽으로 번호를 붙일 수 있다. 부여된 번호는 항상 일정하다.
- 완전 이진 트리(complete binary tree) : 높이가 k일 때, 레벨 1부터 k-1까지는 노드가 채워져 있고, 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진 트리로, 마지막 레벨에서는 노드가 꽉 차 있지 않아도 되지만, 중간에 빈 곳이 있으면 안 된다.
- 정 이진 트리(Full binary tree) : 각 노드가 0개 혹은 2개의 자식 노드를 가진다
- 기타 이진 트리
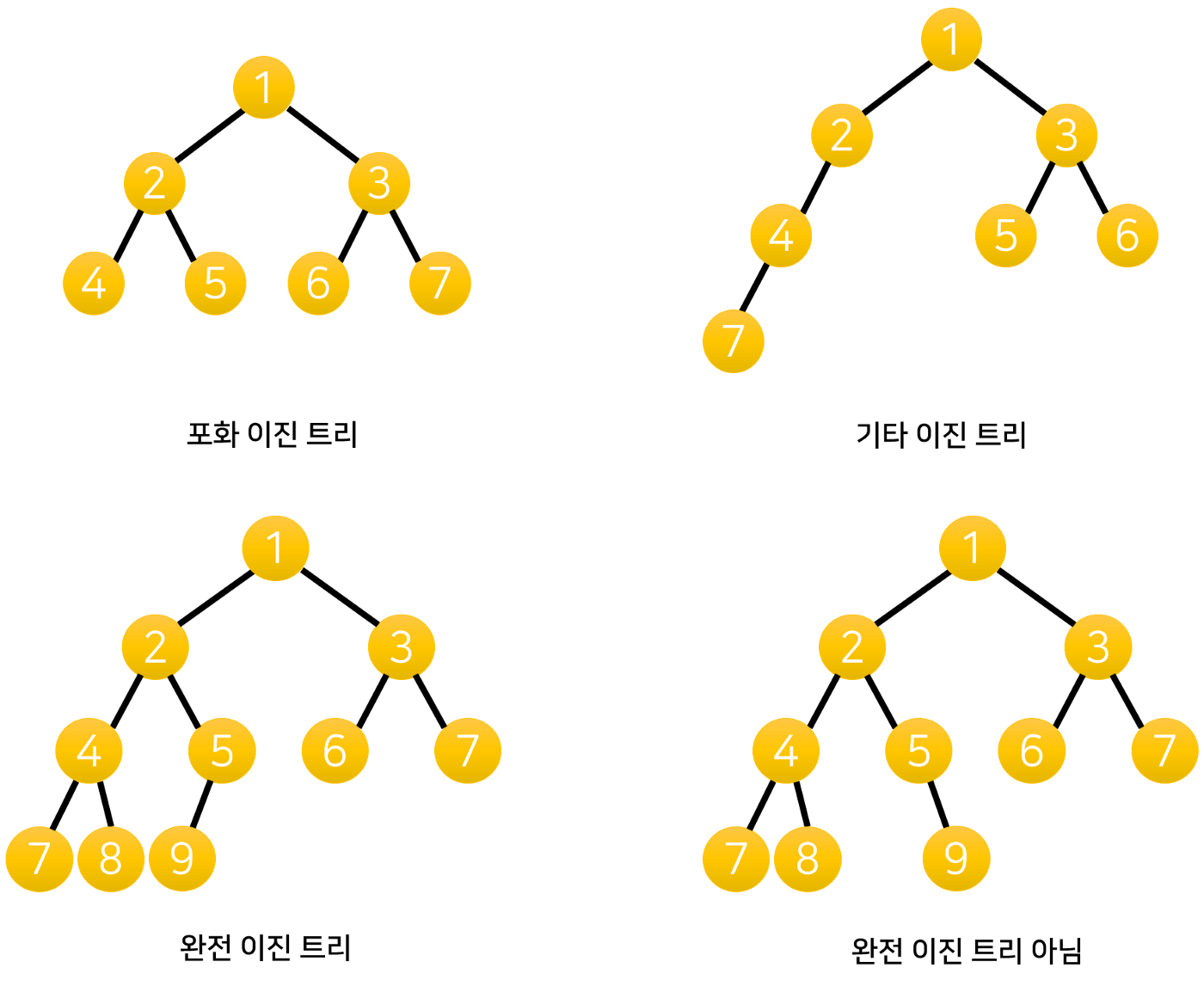

이진 탐색 트리(Binary Search Tree)
이진 탐색 트리란 이진 탐색(binary search)과 연결 리스트(linked list)를 결합한 이진트리를 말한다
이진 탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제가 가능하다.
- 각 노드에 중복되지 않는 키(Key)가 있다
- 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다
- 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다
- 좌우 서브트리도 모두 이진 탐색 트리여야 한다
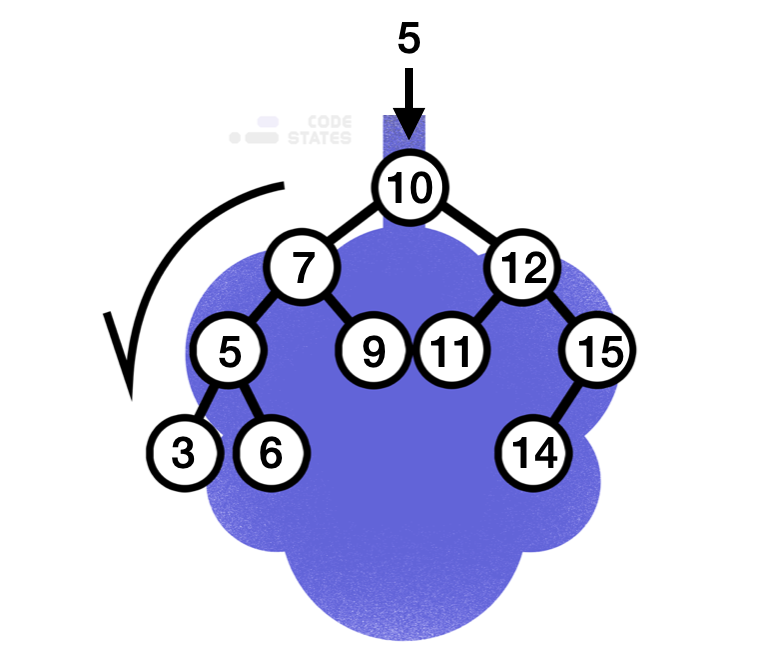
이진 탐색 트리(Binary Search Tree)는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있다
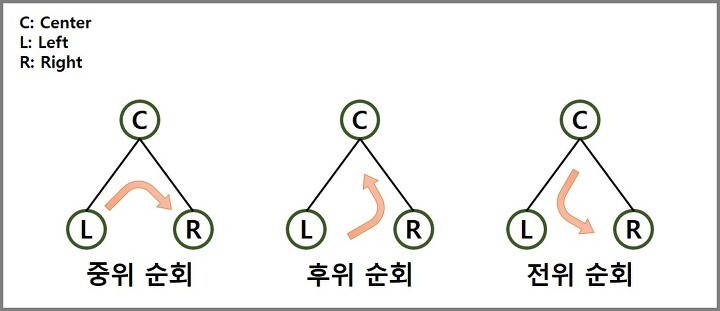
1. 중위 순회: 루트 노드의 왼쪽 자식 노드를 먼저 방문 후에 루트 노드를 중간에 방문하는 방식
2. 후위 순회: 루트 노드의 왼쪽 자식, 오른쪽 자식을 방문 후 루트 노드를 마지막에 방문하는 방식
3. 전위 순회: 루트 노드를 먼저 방문 후 왼쪽 자식, 오른쪽 자식을 방문하는 방식